Convergence Of Arithmetico - Geometric Sequences In Python

Consider the real recursive sequence

\[u_{n+1}=au_n+b\quad(*)\]

defined for every natural number $n$ and some $a,b$ and initial value $u_0$.

This is known in some non Anglo-Saxon countries as an arithmetico-geometric sequence.

In this post we will study the convergence properties of such sequences and visualise the results using Python and Matplotlib.

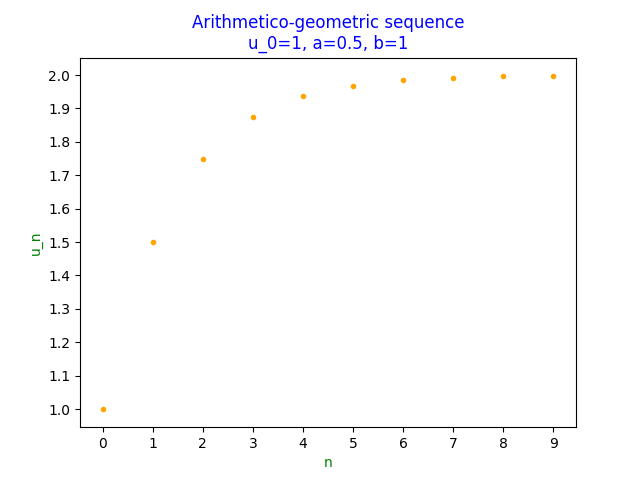
First, let’s print out the first few values of an arithmetico-geometric sequence with $u_0=1,a=\frac{1}{2},b=1$

def arithmetico_geometric(k, u_0=1, a=0.5, b=1):
    i = 0
    current = u_0
    while i < k:
        print(f'u_{i} = {current}')
        current = a * current + b
        i += 1
    return current
    
arithmetico_geometric(10)

which outputs

u_0 = 1
u_1 = 1.5
u_2 = 1.75
u_3 = 1.875
u_4 = 1.9375
u_5 = 1.96875
u_6 = 1.984375
u_7 = 1.9921875
u_8 = 1.99609375
u_9 = 1.998046875

At first glance, this sequence looks like it might be convergent with a limit of 2.

We can visualise the results using Matplotlib

import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np

vectorised_arithmetico_geometric = np.vectorize(
    arithmetico_geometric, otypes=[np.float64])
x = np.arange(0, 10)
y = vectorised_arithmetico_geometric(x)
default_marker_size = mpl.rcParams['lines.markersize'] ** 2
colors = {
  'title': 'blue',
  'marker': 'orange',
  'axis_label': 'green',
}
plt.scatter(x, y, color=colors['marker'], s=default_marker_size / 4)
plt.title('Arithmetico-geometric sequence\nu_0=1, a=0.5, b=1',
          color=colors['title'])
plt.xticks(np.arange(0, 10, 1))
plt.xlabel('n', color=colors['axis_label'])
plt.yticks(np.arange(1, 2.1, 0.1))
plt.ylabel('u_n', color=colors['axis_label'])
plt.show()

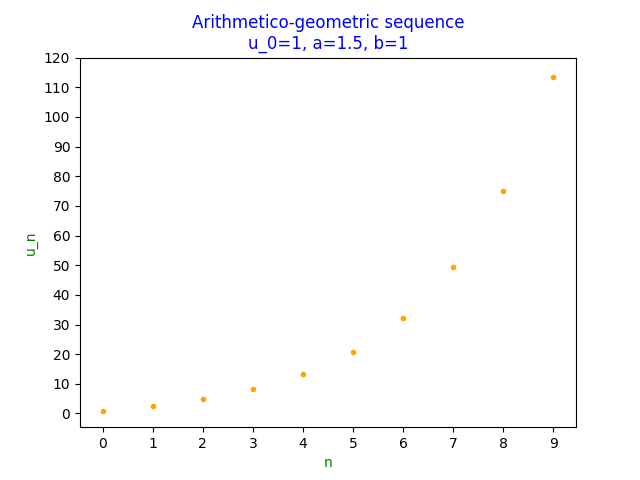
However, setting $a=1.5$ leads to a non convergent looking sequence

Analysis

Intuitively, and from the calculations above, one suspects the convergence of an arithmetico-geometric sequence depends on the value of $a$.

To determine the convergence properties of $(u_n)_{n\geq0}$, we will try to calculate a formula for $u_n$ in terms of $n$ and $u_0$.

Case $a=1$

$(*)$ reduces to

\[u_{n+1}=u_n+b\]

Writing out the first few values, it is clear that

\[u_n=u_0+nb\]

which can be proved by induction.

Case $a\neq1$

Given that

\[x=ax+b\iff x=\frac{b}{1-a}\]

if we denote $v_n=u_n-x$, then

\[v_{n+1}=av_n\]

i.e. $(v_n)_{n\geq0}$ is a geometric sequence with

\[v_n=a^nv_0\]

thus

\[\begin{align} u_n&=v_n+x\\ \iff u_n&=a^nv_0+x\\ \iff u_n&=a^n(u_0-x)+x\\ \iff u_n&=a^nu_0+\frac{b(1-a^n)}{1-a} \end{align}\]

Conclusion

If $a=1$ and $b=0$,

\[u_n=u_0\]

thus

\[\lim_{n\to\infty}u_n=u_0\]

and the sequence is convergent, e.g. $u_0=-5,a=1,b=0$

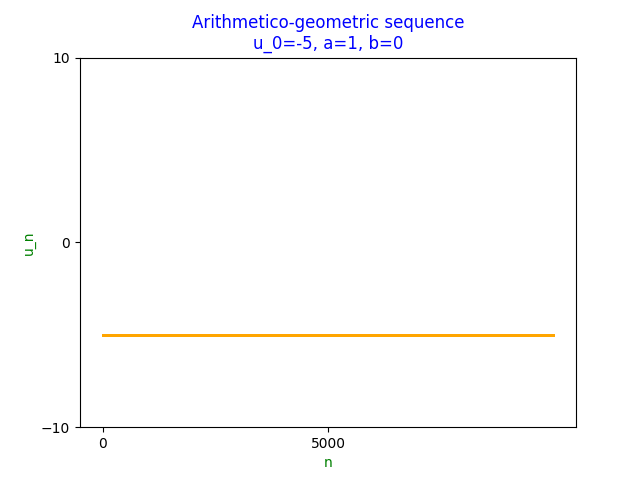
with a limit of -5.

If $a=1$ and $b\neq0$, then

\[\lim_{n\to\infty}u_n=u_0+b\lim_{n\to\infty}(n)\]

Thus the sequence is non convergent, tending to $+\infty$ if $b\gt0$, $-\infty$ otherwise, e.g. $u_0=-5,a=1,b=0.00234742384$

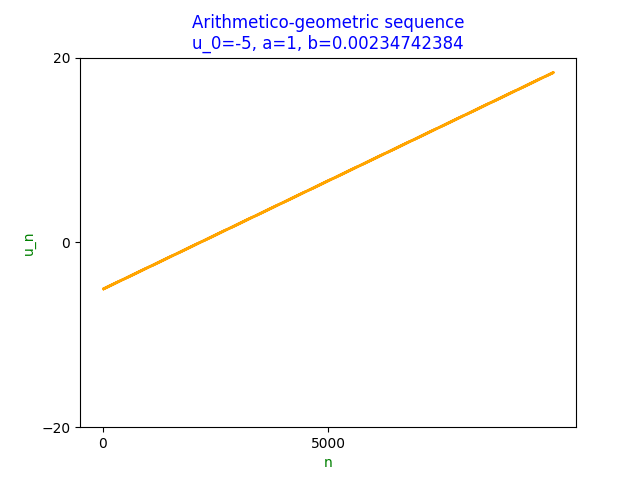
If $a\neq1$,

\[\begin{align} \lim_{n\to\infty}u_n&=\lim_{n\to\infty}\left(a^nu_0+\frac{b(1-a^n)}{1-a}\right)\\ \iff\lim_{n\to\infty}u_n&=u_0\lim_{n\to\infty}(a_n)+\frac{b}{1-a}\left(1-\lim_{n\to\infty}(a^n)\right) \end{align}\]

Thus the sequence is convergent if and only if $\lvert a\rvert\lt1$, e.g. $u_0=-5,a=-0.99324545,b=\pi/6$

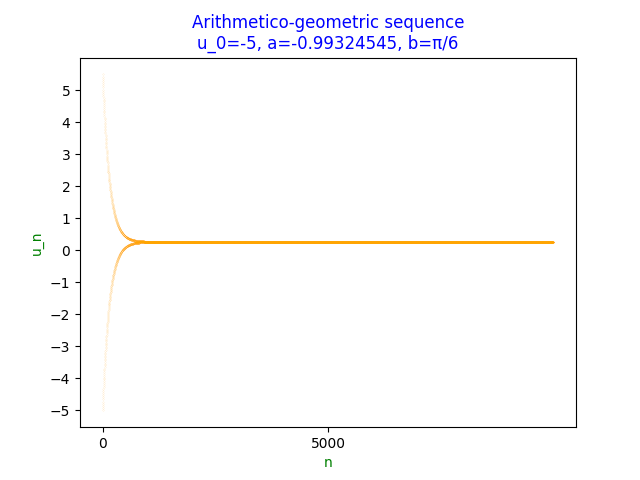
which converges to $l\gt0$.

We can use the function arithmetico_geometric to calculate $u_{10^8}$

print(arithmetico_geometric(10**8))

which outputs

0.262686552525828

which one suspects is a reasonable approximation of $l$.

In fact,

\[l=\frac{b}{1-a}=\frac{\pi/6}{1-(-0.99324545)}=0.2626865525258311\]

which is a difference of

-3.1086244689504383e-15

However, if $\lvert a\rvert\gt1$, e.g. $u_0=-5,a=-1.008999843137,b=\pi/6$

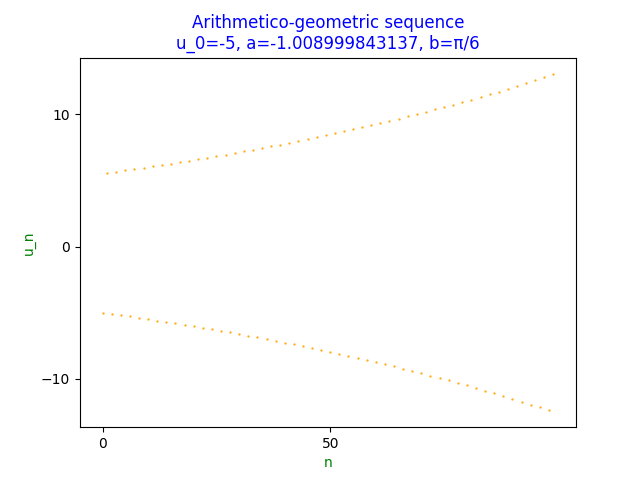
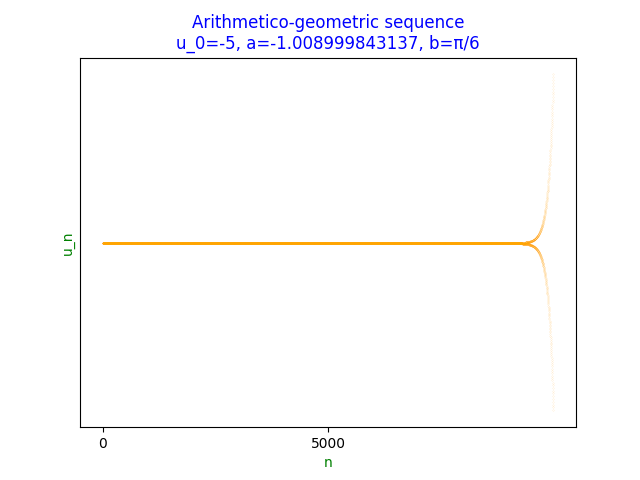
which does not converge.